2024春季学期选了xhz老师的限选课深度强化学习，恰巧也在研究这方面的内容，于是打算写个笔记。

MDP, Value Iteration and Policy Iteration

MDP Basics

Definition of MDP

Markov Decision Process (MDP) 是一个决策过程数学模型，直观地来说：一个智能体 (agent) 处在一个环境中，环境处于不同的状态 (state)；每一步，agent 可以得知环境的部分或全部 state 信息，这部分信息称为 agent 的观测 (observation)；通过 observation，agent 每一步会作出决策，给出一个动作 (action)；这个动作会影响环境，环境有概率转移到另一个 state；同时，环境根据潜在的奖励函数 (rewards) 来给 agent 提供奖励。Formally:

Definition:

An MDP is a 4-tuple $(S, A, T, R)$:

• $S$ is a set of states called the state space.
• $A$ is a set of actions called the action space.
• $T(s, a, s^{\prime})=Pr(s_{t+1}=s^{\prime}|s_t=s, a_t=a)$ is the probability that action $a$ at $s$ leads to $s^{\prime}$, called the transition fuction (also model or dynamics).
• $R(s, a, s^{\prime})$ is the immediate reward received after transitioning from state $s$ to state $s^{\prime}$, due to action $a$.

当然这只是最简单的定义，还可以根据情况的不同引入额外的东西。比如系统初始状态的分布函数 (initial state distribution)，一个一旦到达就直接停止的结束状态 (terminal state)。再比如某些情况下，环境可能是 partially observable 的，agent 无法观测到环境的整个 state (比如打扑克的时候，你无法看到对方手上的牌，这是 partially observable 的，但是下围棋的时候，你可以看到棋盘上所有的东西，这是 fully observable 的)，此时需要在定义中引入 a set of observations $O$，此时的 MDP 称为 Partially Observable MDP (POMDP)。

定义中 Markov 的意思是：给定当前状态之后，未来与过去就无关了，即 $Pr(s_{t+1}|s_t, a_t, s_{t-1}, a_{t-1}, …, s_0)=Pr(s_{t+1}|s_t, a_t)$。可以认为过去的信息都被浓缩到当前的 state 中了。

An Example

用一个简单的例子来加深理解:

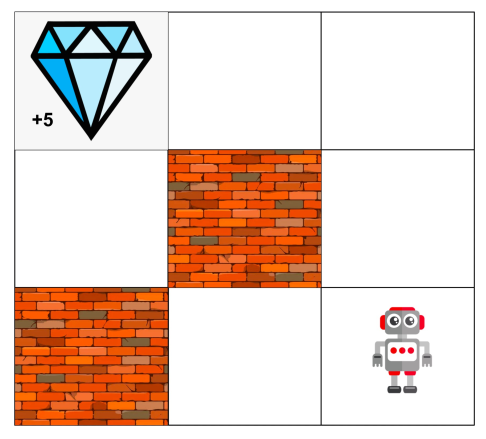
比如一个 agent 位于这样一个 grid world 中

• 每一时刻的 state 就是 agent 的位置。
• action 是上下左右。
• $T$ 我们定义为，有 80% 的可能，agent 的 transition 与其 action 一致；有 10% 的可能，无论什么 action，agent 都往左；有 10% 的可能，无论什么 action，agent 都往右。
• 只有在 agent 吃到钻石的时候才会有 reward。

Policy

以上我们主要关注环境，接下来我们看 agent，我们将 agent 从 state/observation 得到 action 的决策称为 policy:

Definition:

Policy $\pi$ 是一个条件概率密度函数 $\pi(a|s)$，表示 agent 在 state $s$ 时采取 action $a$ 的概率。

Utility

RL 的目标是学出一个好的 policy，那么这个 “好的” 该如何进行评价。直观来看，我们可以将 agent 放在某个 initial state，让其根据自己的 policy 进行运动固定的步数，或是等到最后结束。那么问题就到了，agent 跑出的这个序列 $(s_0, a_0, r_0, s_1, a_1, r_1, …, s_t, a_t, r_t)$ (称为 trajectory) 该如何评价。我们引入 Reward Hypothesis, 即MDP中所有的目标都应被 reward 定义，而不牵扯到其他的量。那么可以将 trajectory 中的 rewards 单独抽出来 $(r_0, r_1, r_2, …, r_t)$。我们希望有一个函数 (Utility) 能够将这个 rewards 序列映射成一个标量，这样有助于比较不同 trajectories 的优劣。

一种方法是直接加起来，即 additive utilities: $U([r_0, r_1, r_2, …]) = r_0+r_1+r_2 + …$

考虑到现实生活中，当下的 reward 往往比之后的 reward 更具有价值 (当下给你一块钱往往优于两天后给你一块钱)，一个更常用的 utility 是 discounted utilities: $U([r_0, r_1, r_2, …]) = r_0+\gamma r_1+\gamma^2 r_2 + …$。其中 $\gamma$ 称为 discounted factor。

Optimal Quantities

直观上定义 optimal quantities:

• Optimal policy: $\pi^*(s)$ = optimal action from state $s$.
• Optimal value/utility of a state $s$: $V^*(s)$ = expected utility starting from $s$ and acting optimally.
• Optimal Q value: $Q^*(s,a)$ = expected utility taking action $a$ from state $s$ and acting optimally.

Formally 可以递归地定义这些量：

$$\pi^{*}(s)=\argmax_a Q^{*}(s,a)$$ $$V^{*}(s)=\max_a Q^{*}(s,a)$$ $$Q^{*}(s,a)=\sum_{s^{\prime}}T(s,a,s^{\prime})[R(s,a,s^{\prime})+\gamma V^{*}(s^{\prime})]$$

从以上两个式子我们可以消去 $Q^{*}$ 得到 $V^{*}$ 满足的等式：

$$V^{*}(s)=\max_a \sum_{s^{\prime}}T(s,a,s^{\prime})[R(s,a,s^{\prime})+\gamma V^{*}(s^{\prime})]$$

称为 Bellman Equation。

Value Iteration

RL 的最终目标是得到 $\pi^{*}$，我们可以利用 $V^{*}$ 来得到 $\pi^{*}$。一种可行的用来得到 $V^{*}$ 的方法称为 Value Iteration，其利用了 Bellman Equation。

假设 MDP 在 $k$ 步后结束，定义 $s$ 的 optimal value 为 $V^{*}_k(s)$，那么有：

$$V_0^{*}(s)=0$$ $$V_{k+1}^{*}(s)=\max_a \sum_{s^{\prime}}T(s,a,s^{\prime})[R(s,a,s^{\prime})+\gamma V_k^{*}(s^{\prime})]$$

迭代计算直至收敛，即可得到 $V_{\infty}^{*}=V^{*}$。

VI 有两个问题：

• VI 每一步的时间复杂度为 $O(S^2A)$，因此仅仅适用于 discrete case，并且要求 $S$ 和 $A$ 均比较小，无法适用于连续空间。
• Policy 往往会比 Value 收敛得更早，如果能够提前发现 policy 已经收敛会更好。

Policy Iteration

Policy Evaluation

上面介绍的 $V^{*}$ 是 optimal policy 的 value function，我们也可以给定一个 policy $\pi$，计算其对应的 value function $V^{\pi}$，这个计算过程称为 Policy Evaluation。

$$V^{\pi}(s) = \text{expected total discounted rewards starting in } s \text{ and following } \pi$$

计算过程类似于 Value Iteration，也是从相应的 Bellman Equation 入手进行迭代计算：

$$V^{\pi}(s)=\sum_{s^{\prime}}T(s,\pi(s),s^{\prime})[R(s,\pi(s),s^{\prime})+\gamma V^{\pi}(s^{\prime})]$$

Policy Evaluation 一步花费时间 $O(S^2)$。

Policy Improvement

假设我们知道一个 MDP 的 value function, 如何得到在这个 value function 下的 optimal policy。显然可以在某个状态 $s$ 遍历所有的 action $a$，看哪个 $a$ 的收益最大，即：

$$\pi(s)=\argmax_a \sum_{s^{\prime}}T(s,a,s^{\prime})[R(s,a,s^{\prime})+\gamma V(s^{\prime})]$$

这个过程就是 policy improvement。

Policy Iteration

结合 Policy Evaluation 和 Policy Improvement，我们可以用另一种方法（不同于 Value Iteration）来得到 $\pi^*$。

循环以下两步直至 policy 收敛：

• Step 1: Policy Evaluation。对当前的 policy 进行 policy evaluation。
• Step 2: Policy Improvement。对 Step 1 中得到的 value function 进行 policy improvement，得到新的 policy。

这就是 Policy Iteration。PI 也可以得到 optimal $\pi^*$，并且在一些情况下比 VI 收敛得更快。

MDP to Reinforcement Learning

不管是 VI 还是 PI，都要求我们知道 MDP 的 $T(s,a,s^{\prime})$ 和 $R(s,a,s^{\prime})$。但是在现实中的大部分情况，我们并不能准确地知道 $T(s,a,s^{\prime})$ 和 $R(s,a,s^{\prime})$，尤其是 $T$，因此需要引入 RL。

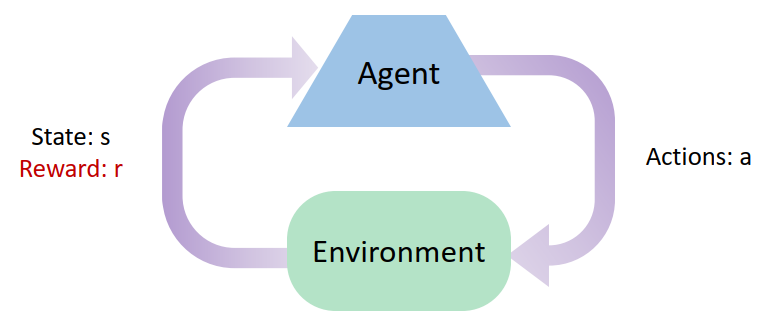
RL 的主要思想是：

• 环境会为 agent 的 action 提供 reward 进行反馈。
• Agent 的所有 utility 都被 reward 定义。
• Agent 的目标是 maximize expected rewards。
• 学习只能基于 agent 获取到的 observations, actions, rewards 等信息（不知道真实的 $T(s,a,s^{\prime})$ 和 $R(s,a,s^{\prime})$）。