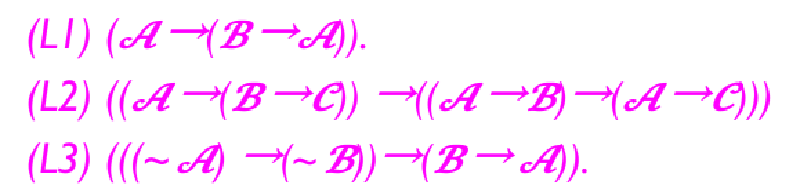Lecture 1 Mathematical Logic (1)
Informal Statement Calculus (非形式的命题演算)
命题、联结词和真值表
自然语言中有许多命题 (statement),比如“拿破仑死了”。而命题之间又可以通过联结词 (connective) 组成更复杂的命题,比如“拿破仑死了并且世界正在欢腾”。在这里,我们假设所有的命题都是非真即假的。常见的联结词及其对应的含义可见下表:
| Meaning | Connectives |
|---|---|
| not $A$ | $\sim A$ |
| $A$ and $B$ | $A \land B$ |
| $A$ or $B$ | $A \lor B$ |
| if $A$ then $B$ | $A \to B$ |
| $A$ if and only if $B$ | $A \leftrightarrow B$ |
“拿破仑死了并且世界正在欢腾”就可以用$A \land B$表示。
各联结词的真值表如下所示:
Negation:
| $p$ | $\sim p$ |
|---|---|
| $T$ | $F$ |
| $F$ | $T$ |
Conjunction:
| $p$ | $q$ | $p \land q$ |
|---|---|---|
| $T$ | $T$ | $T$ |
| $T$ | $F$ | $F$ |
| $F$ | $T$ | $F$ |
| $F$ | $F$ | $F$ |
Disjunction:
| $p$ | $q$ | $p \lor q$ |
|---|---|---|
| $T$ | $T$ | $T$ |
| $T$ | $F$ | $T$ |
| $F$ | $T$ | $T$ |
| $F$ | $F$ | $F$ |
Conditional:
| $p$ | $q$ | $p \to q$ |
|---|---|---|
| $T$ | $T$ | $T$ |
| $T$ | $F$ | $F$ |
| $F$ | $T$ | $T$ |
| $F$ | $F$ | $T$ |
Conditional 的真值表的前两行并不难理解,后两行则可以认为是一种定义上的方便。因为采取这样的定义后,在判断 $p\to q$ 是否恒为真时只需要判断 $p$ 为真是否始终能推出 $q$ 为真即可,而不需要考察 $p$ 为假的情况,这与先前的认知是一致的。
Biconditional:
| $p$ | $q$ | $p \leftrightarrow q$ |
|---|---|---|
| $T$ | $T$ | $T$ |
| $T$ | $F$ | $F$ |
| $F$ | $T$ | $F$ |
| $F$ | $F$ | $T$ |
类似表中的字母 $p, q, r, \cdots$ 称为命题变元 (statement variable),它们表示任意的非特定的单个命题。而由命题变元和联结词组成的表达式称为命题形式 (statement form),定义如下:
Definition:
一个 命题形式 是一个含有命题变元和联结词的表达式,并且能用以下规则构成:
(1) 任何命题变元是一个命题形式。
(2) 如果 $\mathscr{A}$ 和 $\mathscr{B}$ 是命题形式,那么 $(\sim \mathscr{A}), (\mathscr{A} \land \mathscr{B}), (\mathscr{A}\lor \mathscr{B}), (\mathscr{A}\to\mathscr{B}), (\mathscr{A} \leftrightarrow \mathscr{B})$ 是命题形式。
每个命题形式都有其真值表。
Definition:
(1) 一命题形式称为 重言式 (tautology) ,如果对于其中出现的命题变元的各种可能的真值指派,它总取真值为 T 。
(2) 一命题形式称为 矛盾式 (contradiction) ,如果对于其中出现的命题变元的各种可能的真值指派,它总取真值为 F 。
$(p\lor \sim p)$ 是一个重言式,而 $(q\land \sim q)$ 是一个矛盾式。
Definition:
设 $\mathscr{A}$ 和 $\mathscr{B}$ 是命题形式,我们说 $\mathscr{A}$ 逻辑蕴含 (logically implies) $\mathscr{B}$,如果 $(\mathscr{A}\to\mathscr{B})$ 是一重言式,我们说 $\mathscr{A}$ 逻辑等值 (logically equivalent) $\mathscr{B}$,如果 $(\mathscr{A}\leftrightarrow\mathscr{B})$ 是一重言式。
$(p\land q)$ 逻辑蕴含 $p$,$(\sim(p\land q))$ 逻辑等值 $((\sim p)\lor(\sim q))$。
运算和代入规则
Proposition:
如果 $\mathscr{A}$ 和 $(\mathscr{A}\to\mathscr{B})$ 都是重言式,那么 $\mathscr{B}$ 也是重言式。
Proof: omitted.
Proposition (Rules for Substitution):
令 $\mathscr{A}$ 是一个命题形式,其中有命题变元 $p_1, p_2, \cdots, p_n$,并且令 $\mathscr{A}_1, \mathscr{A}_2, \cdots, \mathscr{A}_n$ 是任意命题形式。如果 $\mathscr{A}$ 是一个重言式,那么由 $\mathscr{A}$ 通过用 $\mathscr{A}_i$ 到处去替换每个 $p_i$ 而得到的 $\mathscr{B}$ 也是一重言式。
Proof: omitted.
比如,$(p\land q)$ 逻辑蕴含 $p$,所以对任意 $\mathscr{A}, \mathscr{B}$,都有 $(\mathscr{A}\land \mathscr{B})$ 逻辑蕴含 $\mathscr{A}$。
Proposition (De Morgan’s Law):
令 $\mathscr{A}_1, \mathscr{A}_2, \cdots, \mathscr{A}_n$ 是任意的命题形式,那么:
(1) $(\mathop{\lor}\limits_{i=1}^n (\sim\mathscr{A}_i))$ 逻辑等值于 $(\sim(\mathop{\land}\limits_{i=1}^n \mathscr{A}_i))$
(2) $(\mathop{\land}\limits_{i=1}^n (\sim\mathscr{A}_i))$ 逻辑等值于 $(\sim(\mathop{\lor}\limits_{i=1}^n \mathscr{A}_i))$
Proof:
用数学归纳法,先用 Rules for Substitution 证明 $n=2$ 的情形,再推广至任意正整数 $n$。
范式
Definition:
定义只含有联结词 $\sim, \land, \lor$ 的命题形式为 限制的命题形式 (restricted statement form) 。
Proposition:
每个非矛盾的命题形式逻辑等值于一个限制的命题形式 $\mathop{\lor}\limits_{i=1}^m(\mathop{\land}_{j=1}^n Q_{ij})$,其中每个 $Q_{ij}$ 或是一个命题变元,或是一个命题变元的否定。这个形式称为 析取范式 (disjunctive normal form) 。
每个非重言的命题形式逻辑等值于一个限制的命题形式 $\mathop{\land}\limits_{i=1}^m(\mathop{\lor}_{j=1}^n Q_{ij})$,其中每个 $Q_{ij}$ 或是一个命题变元,或是一个命题变元的否定。这个形式称为 合取范式 (conjunctive normal form) 。
Proof:
仅对析取范式进行证明,合取范式同理。仅需证明任意真值表中只有一行为 $T$ 的命题形式可以用 $\mathop{\land}_{j=1}^n Q_{j}$ 表示即可。多行为 $T$ 的命题形式可由一行为 $T$ 的命题形式通过 $\lor$ 联结得到。
对于每个命题变元 $q_j$,若其在真值表中的那一行取 $T$,则 $Q_{j}=q_j$,否则取 $Q_{j}=\sim q_j$。
这样就可以对任意非矛盾的命题形式构造出一个与其逻辑等值的析取范式。
综合可得:
Proposition:
每个真值函数都可以用一个限制的命题形式表示。
联结词的完全集
Definition:
一个 联结词的完全集 (adequate set of connectives) 是这样一个集合,使得每个真值函数都能由仅仅含有该集中的联结词的命题形式所表示。
显然,$\{\sim, \lor, \land\}$ 是一个完全集。
Proposition:
$\{\sim, \land\}, \{\sim, \lor\}, \{\sim, \to\}$ 都是完全集。
Proof:
可以用 $\{\sim, \lor, \land\}$ 是完全集来证明。
然而,以上介绍的联结词均不能单独构成一个完全集,不过可以通过引入新的联结词来构成只含一个联结词的完全集。
NOR(即 not+or)
| $p$ | $q$ | $p \downarrow q$ |
|---|---|---|
| $T$ | $T$ | $F$ |
| $T$ | $F$ | $F$ |
| $F$ | $T$ | $F$ |
| $F$ | $F$ | $T$ |
NAND(即 not+and)
| $p$ | $q$ | $p | q$ |
|---|---|---|
| $T$ | $T$ | $F$ |
| $T$ | $F$ | $T$ |
| $F$ | $T$ | $T$ |
| $F$ | $F$ | $T$ |
Proposition:
$\{\downarrow\}, \{ | \}$ 都是联结词的完全集。
Proof:
可以用已知的完全集来证明。
但是仅使用一个联结词可能会导致表达式非常复杂,比如仅用 $\downarrow$ 构造出 $(p\to q)$:
$$\{(p\downarrow p)\downarrow [(q\downarrow q)\downarrow (q\downarrow q)]\}\downarrow \{(p\downarrow p)\downarrow [(q\downarrow q)\downarrow (q\downarrow q)]\}$$
论证和有效性
Definition:
论证形式 (argument form) 定义为类似:
$$\mathscr{A}_1, \mathscr{A}_2, \cdots, \mathscr{A}_n; \therefore \mathscr{A}$$
的形式。
我们称一个论证形式是 无效 (nonvalid) 的,如果存在一种对命题变元的真值指派,使得每个 $\mathscr{A}_i$ 均取值 $T$,但是 $\mathscr{A}$ 取值 $F$。否则称其是 有效 (valid) 的。
Proposition:
论证形式 $$\mathscr{A}_1, \mathscr{A}_2, \cdots, \mathscr{A}_n; \therefore \mathscr{A}$$
是有效的,当且仅当命题形式
$$((\mathscr{A}_1\land \mathscr{A}_2 \land \cdots \land \mathscr{A}_n) \to \mathscr{A})$$
是一个重言式。
Proof: omitted.
Formal Statement Calculus (形式的命题演算)
命题演算形式系统 $L$
我们主要关注两个特殊的形式系统(命题演算形式系统、谓词演算形式系统),我们先给出形式系统的一般性定义:
Definition:
一个 形式系统 (formal system) 由以下几部分构成:
(1) 一个符号库 (an alphabet of symbols)。
(2) 这些符号组成的有限字符串(称为合式公式,well-formed fomula)的一个集合。
(3) 合式公式的一个集合,称为公理 (axiom)。
(4) 有限个演绎规则 (rules of deduction) 组成的集合。
接下来给出命题演算形式系统的定义:
Definition:
一个 命题演算形式系统 L (formal system L of statement calculus) 由以下几部分构成:
(1) 一个无限的符号库:
$$\sim, \to, (, ), p_1, p_2, p_3, \cdots$$
(2) 一个合式公式的集合,由以下规则确定:
- 对于每个 $i\geq 1$, $p_i$ 是合式公式。
- 如果 $\mathscr{A}$ 和 $\mathscr{B}$ 是合式公式,那么 $(\sim \mathscr{A})$ 和 $(\mathscr{A}\to\mathscr{B})$ 也是合式公式。
- 所有合式公式都由以上两条规则产生。
(3) 一个公理的集合,对于任何合式公式 $\mathscr{A}, \mathscr{B}, \mathscr{C}$,以下公式是 $L$ 的公理:
- (L1) $(\mathscr{A}\to(\mathscr{B}\to\mathscr{A}))$.
- (L2) $((\mathscr{A}\to(\mathscr{B}\to\mathscr{C}))\to ((\mathscr{A}\to\mathscr{B})\to(\mathscr{A}\to\mathscr{C})))$.
- (L3) $(((\sim \mathscr{A})\to(\sim \mathscr{B}))\to (\mathscr{B}\to\mathscr{A}))$.
(4) $L$ 中仅有一条演绎规则,称为 modus ponens (MP),即对于 $L$ 中的任何公式 $\mathscr{A}$ 和 $(\mathscr{A}\to\mathscr{B})$,$\mathscr{B}$ 也是 $L$ 中的一个公式。
目前而言,在考察 $L$ 中的公式及其演绎时,不应考虑其是否“正确”,而应将其完全视为一文字游戏,只能通过已有公式与演绎规则推出新的合式公式。而至于新推出的合式公式的“正确性”(即新公式为一重言式),则由“公理为重言式”(可直接验证),以及“演绎规则保持公式的重言性”(先前已证明)来保证。
Definition:
$L$ 中的一个 证明 (proof) 是指公式的这样一个序列 $\mathscr{A}_1, \cdots, \mathscr{A}_n$,使得对于每个 $i (1\leq i\leq n)$,或者 $\mathscr{A}_i$ 是 $L$ 的一个公理,或者 $\mathscr{A}_i$ 可由序列中位于 $\mathscr{A}_i$ 前面的两个公式 $\mathscr{A}_j, \mathscr{A}_k (j,k<i)$ 通过 MP 得到。这样的证明称为在 $L$ 中 $\mathscr{A}_n$ 的一个证明,$\mathscr{A}_n$ 称为 $L$ 中的一个 定理 (theorem)。
$\mathscr{A}_n$ 是 $L$ 中的一个定理可记作 $\vdash_L \mathscr{A}_n$。
Exercise:
Prove: $\vdash_L (\mathscr{A}\to\mathscr{A})$.
Solution:
$$\begin{align*} (1)&\quad (\mathscr{A}\to((\mathscr{A}\to\mathscr{A})\to\mathscr{A})) &&(L1)\\ (2)&\quad ((\mathscr{A}\to(\mathscr{A}\to\mathscr{A}))\to(\mathscr{A}\to\mathscr{A})) &&(1)+(L2)+MP\\ (3)&\quad (\mathscr{A}\to(\mathscr{A}\to\mathscr{A})) &&(L1)\\ (4)&\quad (\mathscr{A}\to\mathscr{A}) &&(2)+(3)+MP \end{align*}$$
Definition:
令 $\Gamma$ 是 $L$ 中的公式集(可以是也可以不是 $L$ 中的公理或定理)。$L$ 中的公式序列 $\mathscr{A}_1, \cdots, \mathscr{A}_n$ 是从 $\Gamma$ 的一个 演绎 (deduction),如果每个 $i (1\leq i\leq n)$,下列之一成立:
- $\mathscr{A}_i$ 是 $L$ 的一个公理。
- $\mathscr{A}_i$ 是 $\Gamma$ 中的一个成员。
- $\mathscr{A}_i$ 可由序列中在 $\mathscr{A}_i$ 前的两个公式通过 MP 得到。
记作 $\Gamma\vdash_L \mathscr{A}_n$。
Exercise:
Prove: $\{\mathscr{A},(\mathscr{B}\to(\mathscr{A}\to\mathscr{C}))\}\vdash_L (\mathscr{B}\to\mathscr{C})$.
Solution:
$$\begin{align*} (1)&\quad \mathscr{A} &&假设\\ (2)&\quad (\mathscr{A}\to(\mathscr{B}\to\mathscr{A})) &&(L1)\\ (3)&\quad (\mathscr{B}\to\mathscr{A}) &&(1)+(2)+MP\\ (4)&\quad (\mathscr{B}\to(\mathscr{A}\to\mathscr{C})) &&假设\\ (5)&\quad ((\mathscr{B}\to\mathscr{A})\to(\mathscr{B}\to\mathscr{C})) &&(4)+(L2)+MP\\ (6)&\quad (\mathscr{B}\to\mathscr{C}) &&(3)+(5)+MP \end{align*}$$
注意,这样子推出来的公式并不一定是 $L$ 中的一个定理。
Proposition (The deduction theorem):
$\Gamma\cup\{\mathscr{A}\}\vdash_L\mathscr{B}$ 当且仅当 $\Gamma\vdash_L(\mathscr{A}\to\mathscr{B})$,其中 $\mathscr{A}$ 和 $\mathscr{B}$ 是 $L$ 中的公式,$\Gamma$ 是 $L$ 的公式集(可能是空集)。
Proof:
仅证明从左至右的部分,从右至左可以直接运用 MP。运用数学归纳法证明从左至右的部分,假设从 $\Gamma\cup\{\mathscr{A}\}$ 到 $\mathscr{B}$ 的演绎是一个有 $n$ 个公式的序列。
(1) $n=1$ 时,三种情况:
- $\mathscr{B}$ 是 $L$ 中的一条公理,则有: $$\begin{align*} (1)&\quad \mathscr{B} &&公理\\ (2)&\quad (\mathscr{B}\to (\mathscr{A}\to\mathscr{B})) &&(L1)\\ (3)&\quad (\mathscr{A}\to\mathscr{B}) && (1)+(2)+MP \end{align*}$$
- $\mathscr{B}\in \Gamma$,则同上一种情况。
- $\mathscr{B}=\mathscr{A}$,先前已证 $\vdash_L (\mathscr{A}\to\mathscr{A})$。
(2) 假设从 $\Gamma\cup\{\mathscr{A}\}$ 到 $\mathscr{B}$ 的演绎长度 $< n$ 时,proposition 成立。可以假设 $\mathscr{B}$ 不是 $L$ 中的公理,不在 $\Gamma$ 中,不为 $\mathscr{A}$,那么在 $\Gamma\cup\{\mathscr{A}\}$ 到 $\mathscr{B}$ 的演绎序列中, $\mathscr{B}$ 只可能由先前的两个公式 $\mathscr{C}$ 和 $(\mathscr{C}\to\mathscr{B})$ 通过 MP 得到。故而我们有 $\Gamma\cup \{\mathscr{A}\} \vdash_L \mathscr{C}$ 和 $\Gamma\cup \{\mathscr{A}\} \vdash_L (\mathscr{C}\to\mathscr{B})$。由归纳假设,$\Gamma\vdash_L(\mathscr{A}\to\mathscr{C}), \Gamma\vdash_L(\mathscr{A}\to(\mathscr{C}\to\mathscr{B}))$。由二者,通过 (L2) 和 MP 可得 $\Gamma\vdash_L(\mathscr{A}\to\mathscr{B})$。
这个 proposition 被称为 演绎定理。
Proposition (Hypothetical Syllogism (HS)):
对任何 $L$ 中的公式 $\mathscr{A}, \mathscr{B}, \mathscr{C}$:
$$\{(\mathscr{A}\to\mathscr{B}), (\mathscr{B}\to\mathscr{C})\} \vdash_L (\mathscr{A}\to\mathscr{C})$$
Proof:
$$\begin{align*} (1)&\quad (\mathscr{A}\to\mathscr{B}) &&假设\\ (2)&\quad (\mathscr{B}\to \mathscr{C}) &&假设\\ (3)&\quad \mathscr{A} &&假设\\ (4)&\quad \mathscr{B} &&(1)+(3)+MP \\ (5)&\quad \mathscr{C} &&(2)+(4)+MP \\ \end{align*}$$ 所以有 $\{(\mathscr{A}\to\mathscr{B}), (\mathscr{B}\to\mathscr{C}), \mathscr{A}\} \vdash_L \mathscr{C}$,根据演绎定理,可得 $\{(\mathscr{A}\to\mathscr{B}), (\mathscr{B}\to\mathscr{C})\} \vdash_L (\mathscr{A}\to\mathscr{C})$。
此 proposition 被称为 假言三段论。
Exercise:
Prove:
(1) $\vdash_L(\sim\mathscr{B}\to(\mathscr{B}\to\mathscr{A}))$.
(2) $\vdash_L((\sim\mathscr{A}\to\mathscr{A})\to\mathscr{A})$.
Proof:
(1) $$\begin{align*} (1)&\quad (\sim \mathscr{B}\to(\sim\mathscr{A}\to\sim\mathscr{B})) &&(L1)\\ (2)&\quad ((\sim\mathscr{A}\to\sim\mathscr{B})\to(\mathscr{B}\to\mathscr{A})) &&(L2)\\ (3)&\quad (\sim \mathscr{B}\to(\mathscr{B}\to\mathscr{A})) &&(1)+(2)+HS\\ \end{align*}$$ (2) 由演绎定理,只需证明 $\{(\sim \mathscr{A}\to\mathscr{A})\}\vdash_L \mathscr{A}$: $$\begin{align*} (1)&\quad (\sim\mathscr{A}\to\mathscr{A}) &&假设\\ (2)&\quad (\sim\mathscr{A}\to(\sim\sim(\sim\mathscr{A}\to\mathscr{A})\to\sim\mathscr{A})) &&(L1)\\ (3)&\quad ((\sim\sim(\sim\mathscr{A}\to\mathscr{A})\to\sim\mathscr{A}) \to (\mathscr{A}\to\sim(\sim\mathscr{A}\to\mathscr{A}))) &&(L3)\\ (4)&\quad (\sim\mathscr{A}\to (\mathscr{A}\to\sim(\sim\mathscr{A}\to\mathscr{A}))) &&(2)+(3)+HS\\ (5)&\quad ((\sim\mathscr{A}\to \mathscr{A})\to (\sim\mathscr{A}\to\sim(\sim\mathscr{A}\to\mathscr{A}))) &&(4)+(L2)+MP\\ (6)&\quad ((\sim\mathscr{A}\to\sim(\sim\mathscr{A}\to\mathscr{A})) \to ((\sim\mathscr{A}\to\mathscr{A})\to\mathscr{A})) &&(L2)\\ (7)&\quad ((\sim\mathscr{A}\to\mathscr{A})\to((\sim\mathscr{A}\to\mathscr{A})\to\mathscr{A})) &&(5)+(6)+HS\\ (8)&\quad \mathscr{A} &&(1)+(7)+2\times MP \end{align*}$$
$L$ 的完备性定理
Definition:
$L$ 的一个 赋值 (valuation) 是一个函数 $v$,它的定义域是 $L$ 的公式,值域是集合 $\{T, F\}$,并且使得对 $L$ 的任意公式 $\mathscr{A}, \mathscr{B}$:
(1) $v(\mathscr{A})\neq v(\sim\mathscr{A})$.
(2) $v(\mathscr{A}\to\mathscr{B})=F$ 当且仅当 $v(\mathscr{A})=T$ 和 $v(\mathscr{A})=F$。
Definition:
$L$ 中的一个公式 $\mathscr{A}$ 是一个 重言式,如果对每个赋值 $v$,都有 $v(\mathscr{A})=T$。
Proposition (Soundness,可靠性):
$L$ 中的每个定理都是重言式。
Proof: 数学归纳法。
Proposition (Consistency, 一致性):
$L$ 中的不存在公式 $\mathscr{A}$,使得 $\mathscr{A}$ 和 $(\sim\mathscr{A})$ 都是 $L$ 中的定理。
Proof: Soundness 可以推出 consistency。
Proposition (Adequacy, 完备性):
如果 $\mathscr{A}$ 是 $L$ 中的一个公式,且为重言式,那么 $\mathscr{A}$ 是 $L$ 中的一个定理。
为了证明 adequacy,我们需要引入新的概念。
Definition:
$L$ 的一个 扩充 (extension) 是一个形式系统,它通过修改或者扩大公理组使得原来所有的定理仍是定理(也可能引入新的定理)而得到。
注意,此处说的是 修改 或 扩大,而并不仅仅是 扩大。 一个与 $L$ 没有共同公理的形式系统也可能是 $L$ 的一个扩充。
Proposition:
$L$ 的一个扩充 $L^*$ 是一致的,当且仅当存在一个公式,它不是 $L^*$ 中的定理。
Proof:
(1) 如果 $L^*$ 一致,那么对任意公式 $\mathscr{A}$,总有 $\mathscr{A}$ 或 $(\sim\mathscr{A})$ 不是 $L^*$ 中的定理。
(2) 如果 $L^*$ 不一致,我们证明任意公式 $\mathscr{A}$ 都是 $L^*$ 中的定理。因为存在 $\mathscr{B}$,使得 $\mathscr{B}$ 和 $(\sim\mathscr{B})$ 都是 $L^*$ 中的定理。先前证过 $\vdash_L (\sim\mathscr{B}\to(\mathscr{B}\to\mathscr{A}))$,所以 $\vdash_{L^*} (\sim\mathscr{B}\to(\mathscr{B}\to\mathscr{A}))$。再应用两次 MP 即可得到 $\vdash_{L^*} \mathscr{A}$。
Proposition:
令 $L^*$ 是 $L$ 的一个一致的扩充,并且 $\mathscr{A}$ 是一个公式,它不是 $L^*$ 的一条定理,那么将 $L^*$ 补充公理 $(\sim\mathscr{A})$ 得到的系统 $L^{**}$ 也是一致的。
Proof:
如果 $L^{**}$ 不一致,那么 $\vdash_{L^{**}} \mathscr{A}$,即 $\{\sim\mathscr{A}\}\vdash_{L^*} \mathscr{A}$。
由 deduction theorem,$\vdash_{L^*} (\sim\mathscr{A}\to\mathscr{A})$。
先前有 $\vdash_L ((\sim\mathscr{A}\to\mathscr{A})\to\mathscr{A})$,故 $\vdash_{L^*} \mathscr{A}$。矛盾
由此可知,我们可以依次考察所有公式 $\mathscr{A}$,将 $\mathscr{A}$ 或 $(\sim\mathscr{A})$ 加入公理组中,最终得到一个一致的形式系统,且有对于所有公式 $\mathscr{A}$,都有 $\mathscr{A}$ 或 $(\sim\mathscr{A})$ 是它的定理。
Definition:
$L$ 的一个扩充是 完全 (complete) 的,如果对每个公式 $\mathscr{A}$,都有 $\mathscr{A}$ 或 $(\sim\mathscr{A})$ 是该扩充的一条定理。
Proposition:
存在一个 $L$ 的一致完全扩充。
Proposition:
如果 $L^*$ 是 $L$ 的一个一致完全扩充,那么存在一种赋值使得 $L^*$ 中的每个定理都取值 $T$。
Proof:
定义 $v(\mathscr{A})=T$,如果 $\mathscr{A}$ 是 $L^*$ 中的一条定理,反之定义 $v(\mathscr{A})=F$。用 valuation 的定义可以证明这样的函数是一个 valuation。
Proof of the adequacy theorem of L:
假设 $\mathscr{A}$ 是重言式,但不是 $L$ 的定理,那么可以扩充 $L$ 为 $L\cup\{\sim\mathscr{A}\}$ 再到一个一致完全扩充 $L^*$。$\vdash_{L^*}(\sim\mathscr{A})$,故必定存在赋值 $v$ 使得 $v(\sim\mathscr{A})=T$。矛盾。