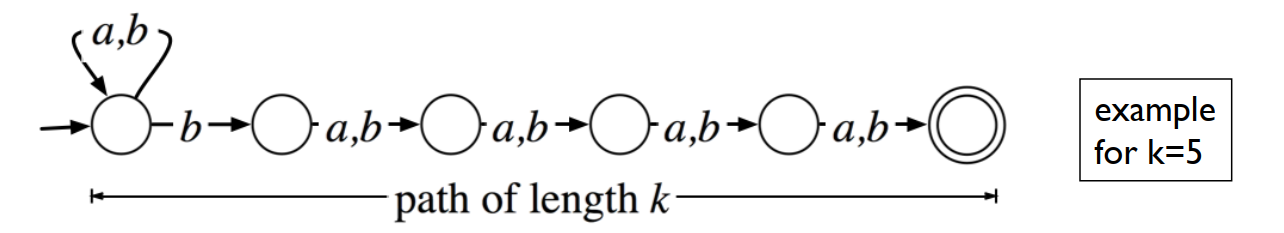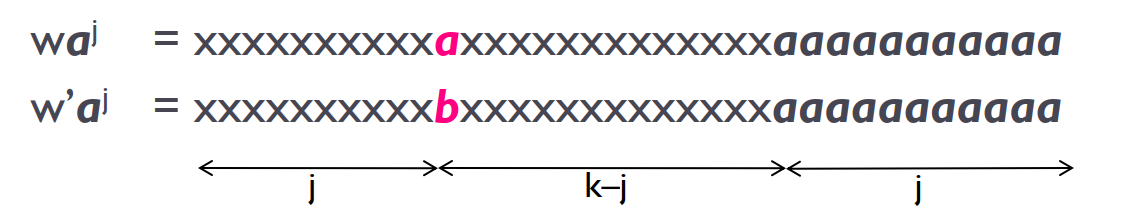Lecture 3 Finite Automata

计算理论剩下的笔记会是 exam-oriented 的，因为系统地写一篇笔记确实太过耗时。

Deterministic Finite Automaton (DFA)

DFA and Regular Languages

Definition:

A DFA is a 5-tuple $(Q, \Sigma, \delta, q, F)$:

• $Q$ is a finite set of states.
• $\Sigma$, the alphabet is a finite set of symbols.
• $\delta: Q\times \Sigma \to Q$ is the transition function.
• $q\in Q$ is the start state.
• $F\subset Q$ is the set of accepting states.

DFA 做的事情就是从 start state 开始，每次从输出序列中获取下一个 symbol，依据 transition function 转成另一个state，直到 inputs 被获取完，判断此时的 state 是否为 accepting state。

Definition:

A DFA $M$ accepts the input $w$ if:

• $M=(Q,\Sigma,\delta,q,F)$.
• $w=w_1 w_2\cdots w_n$, each $w_i\in \Sigma$ for $1\leq i\leq n$.
• $\exists (r_0, r_1, \cdots, r_n)$, each $r_i\in Q$ for $0\leq i\leq n$ s.t.
• • $r_0 = q$, the start state.
• • $r_i = \delta (r_{i-1}, w_i)$, for $1\leq i\leq n$.
• • $r_n\in F$.

每个 DFA 都存在一些 inputs 的集合，使其 accepts，定义这个集合为 DFA 的 language。

Definition:

A Language is a (possibly infinite) set of strings over some alphabet.

$L(M) = \{w | M \text{ accepts } w\}$ is the language recognized by M.

A DFA always recognizes one language!

If it accepts no strings, it recognize the “empty language” $\emptyset$.

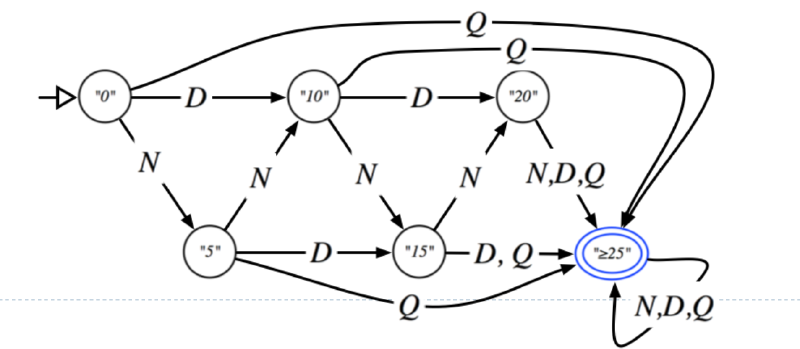
DFA 可以做一些简单的任务，比如判断一个 binary number 是否可以被 3 整除（只需要用 states 存目前被 3 除的余数即可），比如判断一个字母序列是否包含 b（检测到 b 就进入 accepting state）。由此我们可以定义 regular languages：

Definition:

Regular languages is the set of all languages recognized by some DFA.

所以只要一个 language 能被某个 DFA 识别，那它就是一个 regular language。

Regular Languages are Closed under Complementation, Intersection and Union

对于一个或几个 regular language(s)，我们可以由它们构造新的 language，使得新的 language 也是 regular language。比如 complementation: $L^{\prime}=\bar{L}$. 即我们现在已知存在某个 DFA $M$ 使得 $L=L(M)$, 我们是否能找到一个 DFA $M^{\prime}$ 使得 $L(M^{\prime})=\bar(L(M))$。

Theorem:

The class of regular languages is closed under complementation.

Proof:

根据 $M$, 构造一新的 DFA $M^{\prime}$，二者完全一样，除了 $M^{\prime}$ 的 accepting states 是 $M$ 的 accepting states 的补集。这样的话一个 input 能被 $M$ 识别当且仅当其不能被 $M^{\prime}$ 识别。

Theorem:

The class of regular languages is closed under intersection.

Proof:

假设我们现在有两个 DFAs $M_1=(Q_1, \Sigma, \delta_1, s_1, F_1), M_2=(Q_2, \Sigma, \delta_2, s_2, F_2)$，构造一新 DFA $M_3=(Q_1\times Q_2, \Sigma, \delta_1\times \delta_2, (s_1,s_2), F_3)$。即 $M_3$ 的状态空间是 $Q_1$ 和 $Q_2$ 的直积，在两个分量空间中分别作 transition。$(q_1, q_2)\in F_3$ 当且仅当 $q_1\in F_1, q_2\in F_2$。

Theorem:

The class of regular languages is closed under uniton.

Proof:

可以用 DeMorgan’s Law $X\cup Y = \overline{(\bar{X}\cap\bar{Y})}$，也可以用与上一 theorem 类似的构造。

定义 regular operations on languages:

Definition: A & B are two (possibly infinite) sets of strings. Define regular operations on them:

• Union: $A \cup B = \{x | x\in A \text{ or } x\in B\}$.
• Concatenation: $A\circ B = \{xy | x\in A \text{ and } y\in B\}$.
• Star: $A^* = \{x_1 x_2 \cdots x_k | k\geq 0 \text{ and all } x_i\in A\}$.
• • note: the empty string $\epsilon (k=0)$ is always in $A^*$.

我们已知 regular languages is closed under union，但对剩下两种 operations，很难直接构造出合适的 DFA，需要先引入新的概念。

Nondeterministic Finite Automaton (NFA)

NFA

NFA 与 DFA 类似，但它

• 可以不获取输入自发转变状态（也可以被视作获取空字符 $\epsilon$）。
• 在某个状态获取某个输入之后，转变成的新状态有很多种可能。

Definition:

An NFA is a 5-tuple $(Q, \Sigma, \delta, q, F)$:

• $Q$ is a finite set of states.
• $\Sigma$, the alphabet is a finite set of symbols.
• $\delta: Q\times \Sigma_{\epsilon} \to 2^Q$ is the transition function.
• $q\in Q$ is the start state.
• $F\subset Q$ is the set of accepting states.

这里，$\Sigma_{\epsilon}=\Sigma\cup\{\epsilon\}$，$2^Q$ 是 $Q$ 的所有子集组成的集合，叫做 $Q$ 的 power set。

Definition:

An NFA $N$ accepts the input $w\in \Sigma^*$ if:

• $N=(Q,\Sigma,\delta,q,F)$.
• $w$ can be written as $x_1 x_2\cdots x_n$, each $x_i\in \Sigma_{\epsilon}$ for $1\leq i\leq n$.
• • 注意这里用的是 “can be written” 而不是 “="，因为 $“abba”$ can be written as $“a\epsilon bb \epsilon a”$。
• $\exists (r_0, r_1, \cdots, r_n)$, each $r_i\in Q$ for $0\leq i\leq n$ s.t.
• • $r_0 = q$, the start state.
• • $r_i \in \delta (r_{i-1}, x_i)$, for $1\leq i\leq n$.
• • $r_n\in F$.

Equivalence of NFA and DFA

可以证明 NFA 与 DFA 是等价的，即对任意 NFA 都可以找到一个 DFA，使得二者的 language 相同；对任意 DFA 也可以找到一个 NFA，使得二者的 language 相同。后者是显然的，因为任意 DFA 本身就可以被视为一个 NFA。我们现在要证明前者。

Theorem:

For any NFA $N$, there is a DFA $M$ such that $L(N) = L(M)$.

Proof:

总的思想就是：at all times, M keeps track of the set of states that N could be in.

(1) 先对 $N$ 中不存在 $\epsilon$ 的情况证明：

若 $N=(Q,\Sigma,\delta,q,F)$，令 $M=(Q^{\prime}, \Sigma, \delta^{\prime}, q^{\prime}, F^{\prime})$:

• $Q^{\prime}=2^{Q}$
• $\delta^{\prime}(R,a)=\cup_{r\in R}\delta(r,a)$。其中 $R\in 2^{Q}, a\in \Sigma$。
• $q^{\prime}=\{q\}$
• $F^{\prime}=\{R\in Q^{\prime} | R\cap F\neq \emptyset\}$

(2) 对于存在 $\epsilon$ 的情况，可以将 $\epsilon$ 后的 state 并入前面的 state。Formally:

令 $E(R)=\{r\in Q | r \text{ is reachable from } R \text{ using zero on more } \epsilon \text{-transitions}\}$.

• $Q^{\prime}=2^{Q}$
• $\delta^{\prime}(R,a)=\cup_{r\in R}E(\delta(r,a))$。其中 $R\in 2^{Q}, a\in \Sigma$。
• $q^{\prime}=E(\{q\})$
• $F^{\prime}=\{R\in Q^{\prime} | R\cap F\neq \emptyset\}$

一个 NFA 需要 $\log_2 |Q|$ bits 来存 states，与其等价的 DFA 需要 $\log_2 |Q^{\prime}| = |Q|$ bits 来存 states。可以举出一个 NFA 的例子，证明这样的 exponential blowup 在某些情况下是必须的。

Example:

$\Sigma=\{a,b\}, L_k=\{w\in\{a,b\}^* | \text{ the } k \text{-th symbol from the end is } b\}$. There is a $(k+1)$-state NFA recognizing $L_k$.

Then we prove that any DFA with $< 2^k$ states can not recognize $L_k$.

We prove by contradiction.

(1) Assume there is a DFA $M$ with $|Q| = 2^k - 1$.

(2) Imagine running $M$ on each input $w\in\{a,b\}^k$.

(3) By the pigeonhole principle, $\exists w \neq w^{\prime}\in\{a,b\}^k$ s.t. after reading $w$ and $w^{\prime}$, $M$ is in the same state.

(4) Let $j+1$ be the first position where $w$ and $w^{\prime}$ differ.

(5) Run $M$ on $wa^j$ and $w^{\prime}a^j$. $M$ is supposed to be in the same state. But $w\notin L_k, w^{\prime}\in L_k$. A contradiction.

Regular Languages are Closed under Concatenation and Star

先介绍定理：

Theorem:

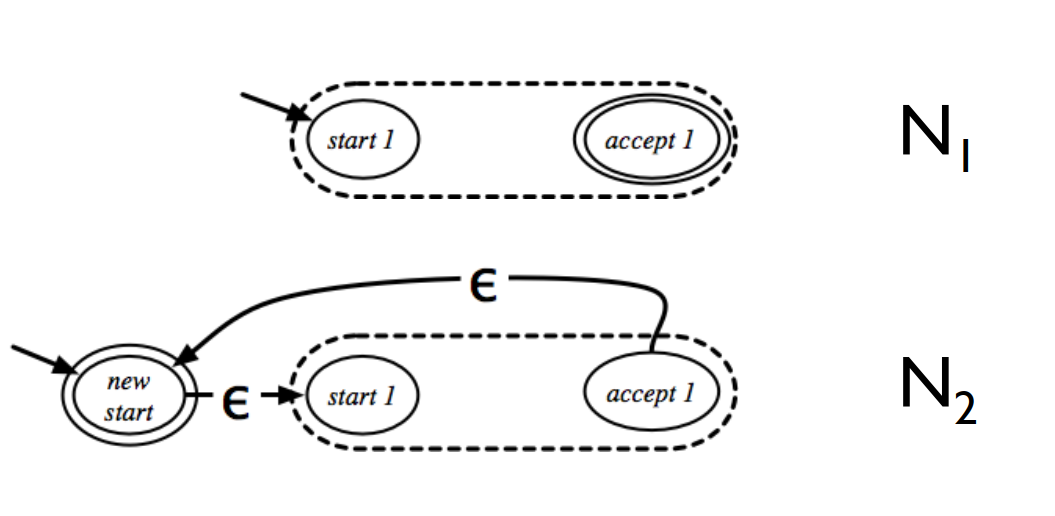
For any NFA $N_1$, there is an NFA $N_2$ such that $L(N_1) = L(N_2)$ and $N_2$ has exactly one accept state.

Proof:

把 $N_1$ 中所有的 accepting states 用 $\epsilon$ 连到一个新的 accepting states。

Theorem:

The class of regular languages is closed under concatenation.

Proof:

对于 $N_1, N_2$ 构造 $N_3$ 使得 $L(N_3)=L(N_1)\circ L(N_2)$。只需要把 $N_1$ 的 accepting states 都用 $\epsilon$ 连到 $N_2$ 的 starting state 就行。

Theorem:

The class of regular languages is closed under star。

Proof:

如下图构造 $L(N_2)=L(N_1)^*$:

Equivalence of NFAs, DFAs and Regular Expressions

Definition:

一个 regular expression (REGEXP) 是用以下方式表示的一个集合： 从 $\{a\}, \{\epsilon\}, \emptyset$ 开始，通过 $(R_1\cup R_2), (R_1\circ R_2), (R_1^*)$ 构成。

简化：省略 $\circ$，定义计算顺序 $^*, \circ, \cup$。

接下来证明 REGEXP 和 NFA 等价。

Theorem:

(1) The language of any REGEXP is recognized by an NFA.

(2) The language of any NFA can be represented by a REGEXP.

(1) 是显然的，因为 regular languages are closed under $\cup, \circ, ^*$。

(2) 不显然，需要引入新概念。

Definition:

A GNFA (Generalized NFA) is a 5-tuple $(Q, \Sigma, \delta, q_{start}, q_{accept})$:

• $Q$ is a finite set of states.
• $\Sigma$, the alphabet is a finite set of symbols.
• $q_{start}$ is the start state.
• $q_{accept}$ is the accept state.
• $\delta: (Q\backslash \{q_{accept}\}) \times (Q\backslash \{q_{start}\}) \to REGEXP$ is the transition function.

简单地说，GNFA 就是 NFA，只不过 transition 用 REGEXP 表达。显然 GNFA 和 NFA 等价。

故而，证明 (2) 的思路为：任意一个 NFA 都可以用一个 GNFA 表示，任意一个 GNFA 都可以被缩减为只有两个 states，所以等价于一个 REGEXP。第一步和第三步显然。第二步逐个删去 state 即可，图解：

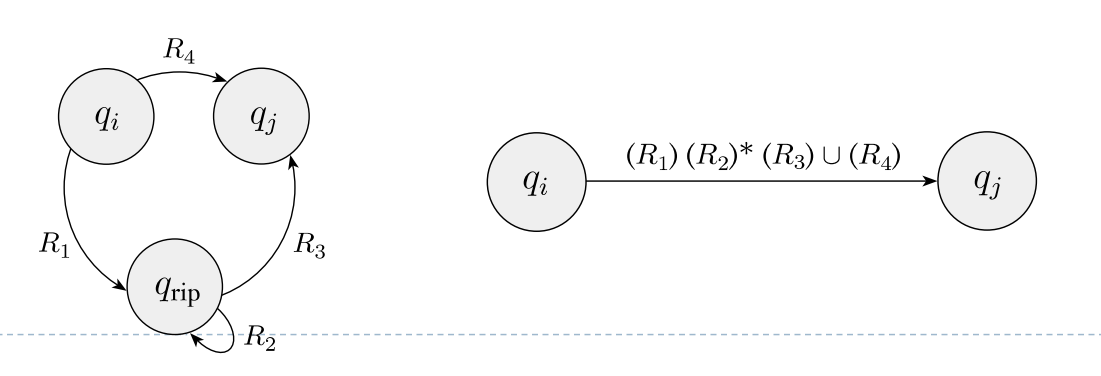
Nonregular Languages

Example:

\{0^n 1^n|n\geq 0\} is nonregular.

Proof:

Assume it’s regular, the DFA recognizing it consists of $p$ states. Then by the pigeonhole principle, there exists $i,j$ such that after reading $0^i, 0^j$, the DFA is in the same state. So if it accepts $0^i 1^i$, it must accept $0^j 1^i$, which is a contradiction.

用这种思想，可以引入 pumping lemma:

Pumping Lemma:

If $A$ is a regular language, then there is a number $p$ (the pumping length) where, if $s$ is any string in $A$ of length at least $p$, then $s$ can be divided into $s=xyz$, satisfying:

• For each $i\geq 0, xy^i z \in A$
• $|y|>0$
• $|xy|\leq p$

Proof:

令 $p$ 是 DFA 的状态数，再用上面那个例子中类似的思想即可。

可以用 pumping lemma 判断 nonregular language。如果不满足 pumping lemma，那么肯定是 nonregular language。思路就是，假设有个 $p$，再从 language 中找反例。

可以证明 $\{ww|w\in \{0,1\}^*\}, \{1^{n^2}|n\geq 0\}, \{0^i 1^j|i>j\}$ 都是 nonregular language。