Lecture 4 Context-Free Grammar
Context-Free Grammar
We have already known that REGEXPs can generate languages. Now we introduce another way to generate languages: Context-free grammar (CFG).
Definition:
A CFG is a 4-tuple $(V, \Sigma, R, S)$:
- $V$ is a set of variables.
- $\Sigma$ is a set of terminals.
- $R$ is a set of rules (a rule consists of a variable and a sting in $(V\cup \Sigma)^*$).
- $S$ is the start variable.
We say $uAv$ yields $uwv$ ($uAv \Rightarrow uwv$) if $A\to w$ is a rule in $R$.
We say $u$ derives $v$ ($u \Rightarrow^* v$) if $\exists u_1, u_2, \cdots, u_k$ such that $u\Rightarrow u_1\Rightarrow u_2\Rightarrow\cdots\Rightarrow u_k \Rightarrow v$.
总的来说,CFG 就是从 $S$ 开始,每次从现在的字符串中选择一个 variable,依据某个 rule 将其替换为一个 string,直到没有 variable 为止。
Definition:
The language of a CFG $G$ is defined as:
$$L(G)=\{w\in \Sigma^* | S\Rightarrow^* w\}$$
CFG is more powerful than DFA
要证明 CFG is strictly more powerful than DFA,要从两方面入手:
- (1) 存在 language,可以用 CFG 表达,但不是 regular language。
- (2) 任意 regular language 都可以用 CFG 表达。
对于 (1),上节课已知 $L=\{0^n1^n | n\geq 0\}$ is nonregular,但可以用 CFG $S\to 0S1|\epsilon$ 得到。
对于 (2),即要证明:
Theorem:
Given a DFA $A=(Q,\Sigma,\delta,q_0,F)$, we can find a CFG $A^{\prime}=(V,\Sigma^{\prime},R,S)$, such that $L(A)=L(A^{\prime})$.
Proof:
- 对 $A$ 的每个 state $q_i$,在 $V$ 中引入一个变量 $R_i$。
- 如果 $\delta(q_i,a)=q_j$,就在 $R$ 中引入 rule $R_i\to a R_j$。
- $q_0$ 是 starting state,那么 $R_0$ 就是 start variable。
- 如果 $q_i$ 是一个 accepting state,就在 $R$ 中加入 rule $R_i\to\epsilon$。
这样构造出来的 $A^{\prime}$ 满足 $L(A)=L(A^{\prime})$。
An example:

Parse Trees and Ambiguity
可以用一个 parse tree 来表示从 start variable 生成一个 string of terminals 的过程:
Definition:
Parse tree:
- Each internal node labeled with a variable.
- Each leaf labeled with a terminal.
- The children of a node represent the rule that was applied.
An example:
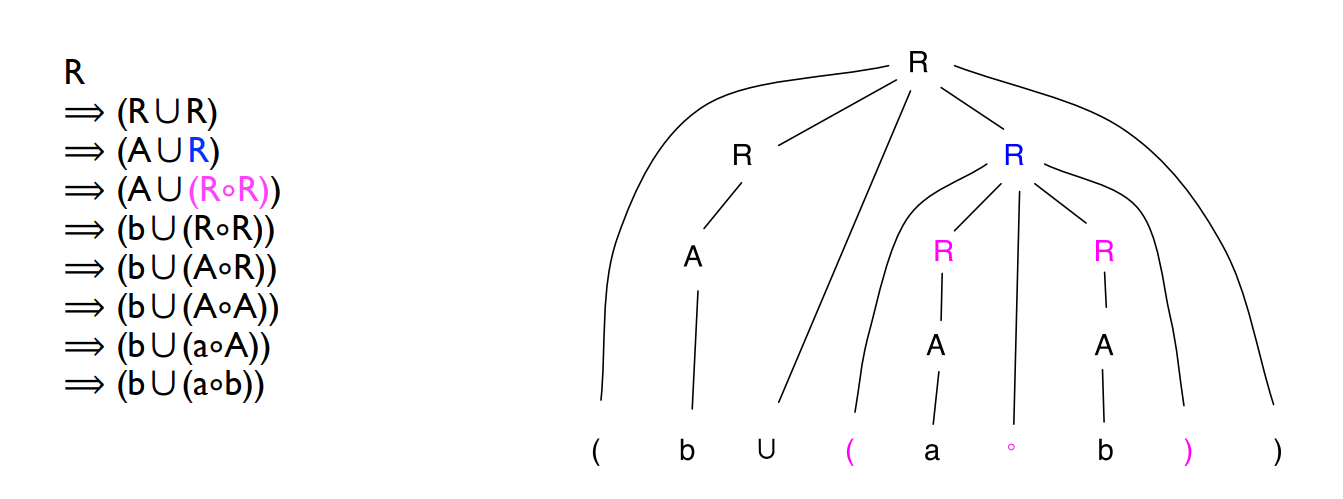
Definition:
A CFG is called ambiguous if a string has two distinct parse trees.
直观上来说,ambiguous 指的就是存在歧义,比如 $a+a\times a$,如果不定义 + 和 $\times$ 的计算顺序,就有可能先算 +,也可能先算 $\times$。
ambiguous 并不等同于 “存在两种 derivations”,因为两种 derivations 可能对应同一个 parse tree。
Definition:
Leftmost derivation: 每一步替换当前 string 最左边的那个 variable。
Theorem:
ambiguous 等价于存在两种 leftmost derivations。
Definition:
A CFL (context free language, 即可以用某个 CFG 生成的 language) is called inherently ambiguous if every CFG of it is ambiguous.
An example of inherently ambiguous CFL:
$$L=\{w | w=a^ib^jc^k, i,j,k\geq 1 \text{ and } i=j \text{ or } i=k\}$$
Closure Properties
Theorem:
CFLs are closed under Union, Concatenation, Kleene Star.
Proof:
只需要在原先的 CFG 之上引入新的 start variable,用新的 start variable 去生成旧的 start variables即可。
Theorem:
CFLs are NOT closed under intersection. But CFLs are closed under intersection with REGULAR languages.
Proof:
$$L = \{w : w \in \{0, 1\}^*, w \text{ is a palindrome, and } w \text{ contains fewer 0s than 1s }\}$$
这是两个 CFL 的 intersection,可以用后面将要介绍的 pumping lemma 证明它不是 CFL。
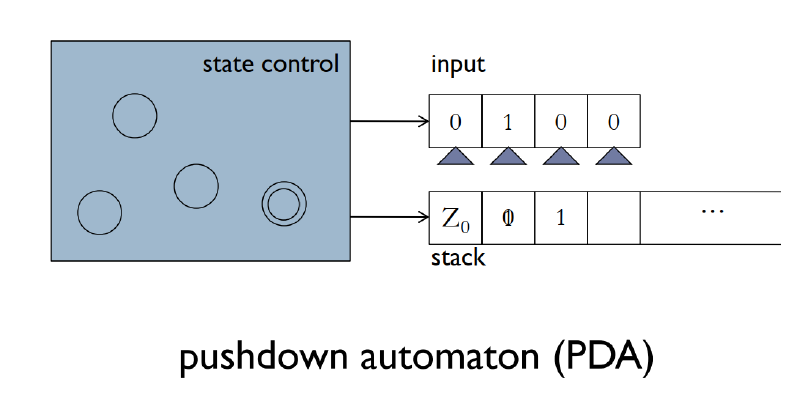
Pushdown Automaton (PDA)
Regular language 在句法上可以用 REGEXP 生成,在计算模型上可以被 DFA、NFA 识别。CFL 在句法上可以用 CFG 生成,现引入新的计算模型 PDA 来识别 CFL。
由于 CFL 是 regular language 的扩充,PDA 也应该是 NFA 的扩充。事实上,PDA 就是为 NFA 多提供了一个无穷大的 stack,PDA 读取 input 的时候,可以从 stack 中 push 或 pop 一个 symbol。
PDA 做的事情就是,每次读取一个 input(可能是 $\epsilon$),并从 stack 顶部 pop 出一个 symbol(可能是 $\epsilon$),然后 transit to a new state and push a symbol to the top of the stack(可能是 $\epsilon$)。
Definition:
A pushdown automaton (PDA) is a 6-tuple $(Q, \Sigma, \Gamma, \delta, q_0, F)$:
- $Q$ is a finite set of states.
- $\Sigma$ is the input alphabet.
- $\Gamma$ is the stack alphabet.
- $q_0$ in $Q$ is the initial state.
- $F \subseteq Q$ is a set of final states.
- $\delta$ is the transition function.
- $\delta : Q \times (\Sigma \cup \{\epsilon\}) \times (\Gamma \cup \{\epsilon\}) \to 2^{Q \times (\Gamma \cup \{\epsilon\})}$
Definition:
PDA $(Q, \Sigma, \Gamma, \delta, q_0, F)$ accepts string $w \in \Sigma^*$ if:
- $w$ can be written as $x_1 x_2 \cdots x_m$, each $x_i \in \Sigma \cup \{\epsilon\}$.
- $\exists r_0, r_1, \cdots, r_m \in Q$, a sequence of $m+1$ states.
- $\exists s_0, s_1, \cdots, s_m \in \Gamma^*$, stack contents.
- such that
- $r_0 = q, s_0=\epsilon$.
- $(r_i, b) \in \delta(r_{i-1},x_i, a)$, where $s_{i-1}=ta$ and $s_i=tb$ for $1 \leq i \leq m$.
- $r_m\in F$.
可以通过构造 PDA 的方法证明 $$L=\{ww^R\}$$ $$L=\{w:w=w^R\}$$ $$L=\{w: w \text{ has the same number of 0s and 1s}\}$$ $$L=\{w: w \text{ has two 0-blocks with same number of 0s}\}$$ 都可以被 PDA 识别。
Equivalence of CFG and PDA
Theorem:
A language L is context-free if and only if it is accepted by some pushdown automaton.
Proof:
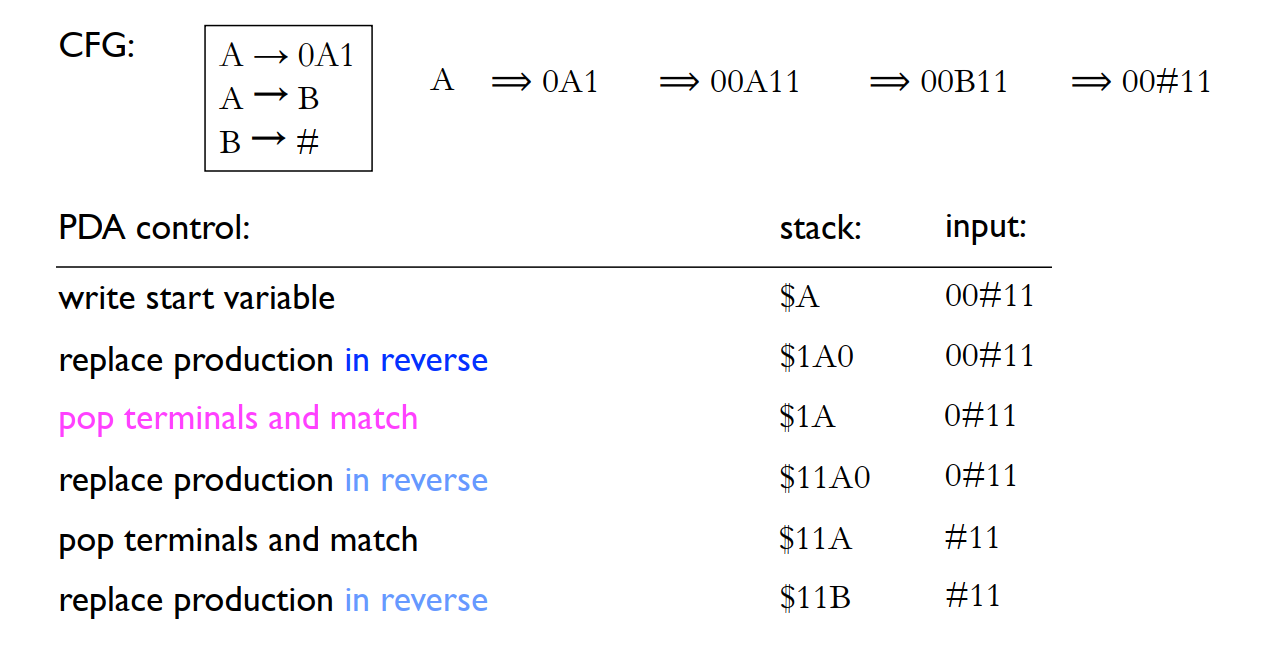
(1) From CFG to PDA. 思路就是用 PDA 来模拟 leftmost derivation。将每时每刻的 string 倒序放在 stack中,如果 stack 的顶部是 terminal,就和 input 比较,相同则 pop out,不同则 reject;如果 stack 顶部是 variable,就做 leftmost derivation。
例子:
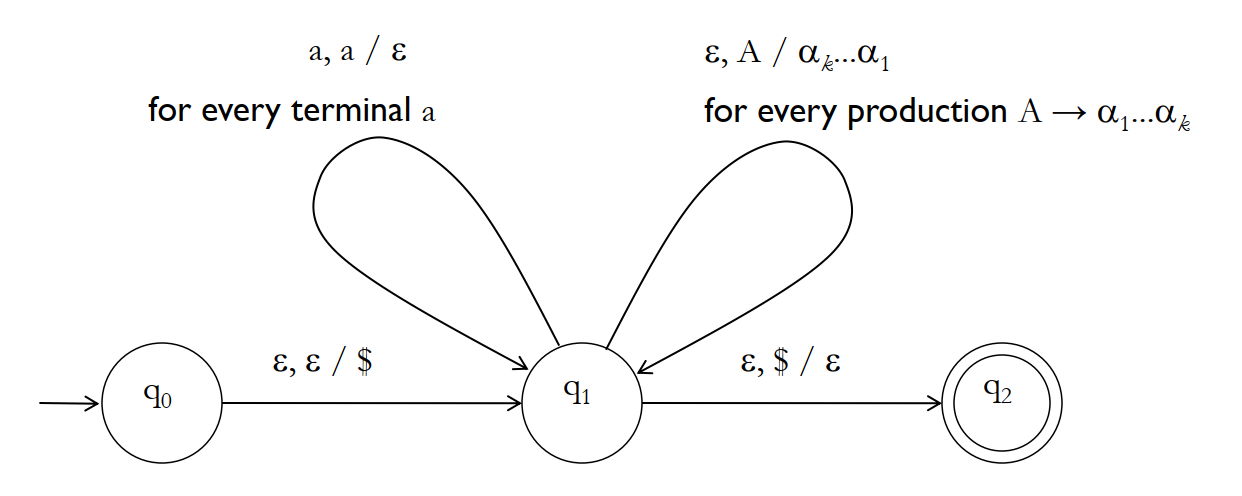
Formally:
用图来表示 PDA 就是:
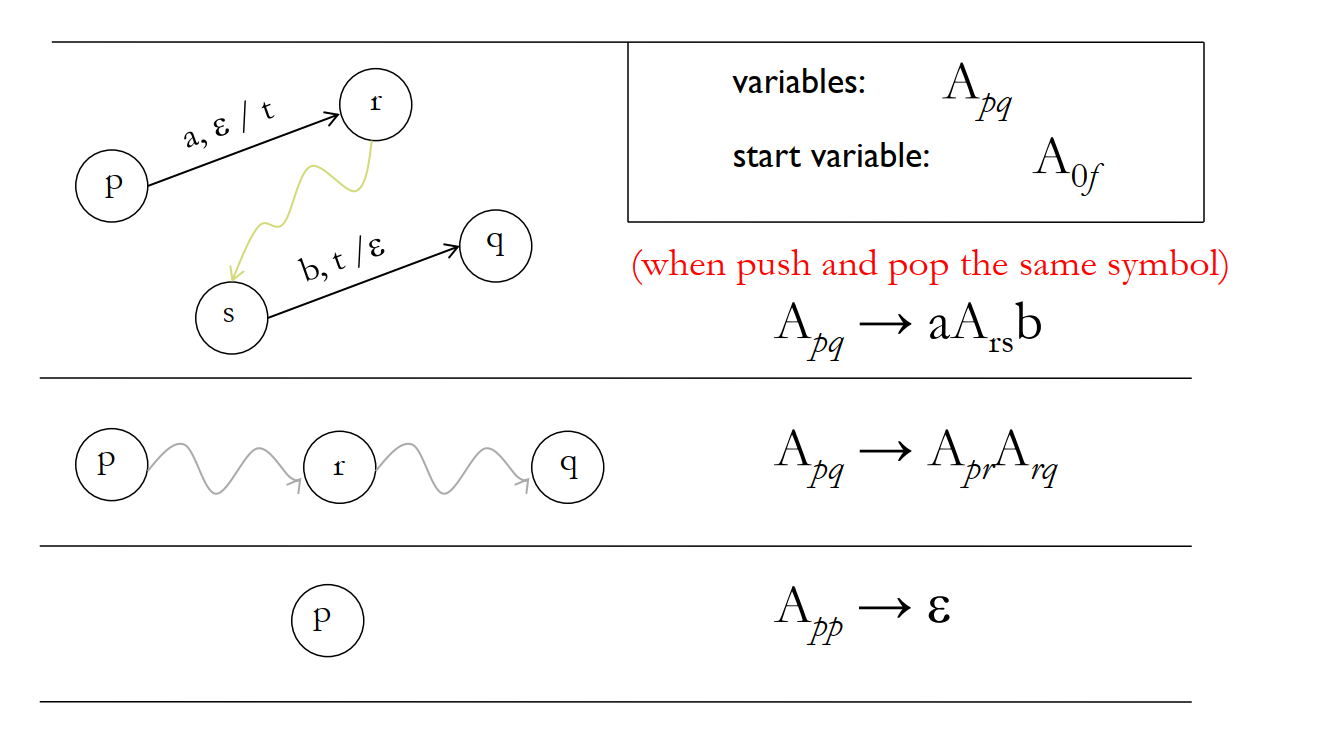
(2) From PDA to CFG. 总的思路就是,先令 PDA 只有一个 accept state,并且 accept 之前会清空 stack。然后 CFG 的一个 variable 就是一个字符串的集合,使得 PDA 读取集合中的字符串能从某个 state 转移到另一个 state,同时保持 stack 不变。
Formally:
CFG 的 rules 如下:
并不给出详细的证明,直观理解即可。
Chomsky Normal Form and CYK algorithm
Definition:
A context-free grammar is in Chomsky normal form if every rule is of the form:
- $A \to BC$
- $A \to a$
其中,$A, B, C$ 是任意 variables,$a$ 是任意非 $\epsilon$ 的 terminal。$B, C$ 不能是 start variable。允许 $S\to \epsilon$。
任意 CFG 都可以转换成 CNF 的形式,课件的 91-98 页讲得很清楚,还举了个例子。
将任意 CFG 转成 CNF 之后,我们就可以用 Cocke–Younger–Kasami algorithm 来判断某个特定的 string 能否被某个特定的 CFG 生成。假设 string 为 $s[1:n]$,CFG 有 $r$ 个 variables $R$,其中 $R_1$ 是 start variable。总的思路是,构造一个 $n\times n\times r$ 的表格 $T$,其中 $T[i,j,k]$ 表示 $s[i:j]$ 能否由 $R_k$ 生成,然后依据 $j-i$ 从小到大的顺序 DP 地判断 $s[i:j]$ 能否被 $R_k$ 生成。最后,$s$ 能被生成当且仅当 $T[1,n,1]$ 为真。
Pumping Lemma for CFL
Theorem:
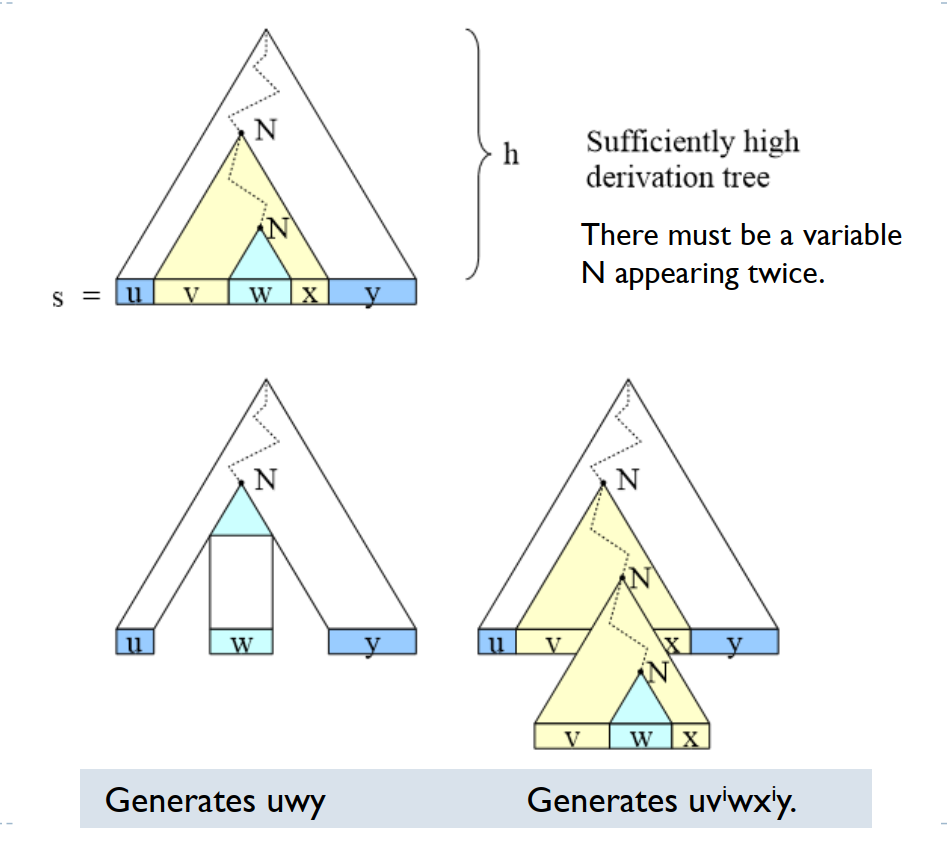
If $A$ is a context-free language, then there is a number $p$ (the pumping length) where, if $s$ is any string in $A$ of length at least $p$, then $s$ may be divides into 5 pieces $s=uvxyz$, satisfying:
- For each $i\geq 0, uv^ixy^iz \in A$
- $|vy|> 0$
- $|vxy|\leq p$
Proof:
用 CFG 来证明,假设 CFG 有 $a$ 个 variables,rules 右手边的 symbols 最长为 $b$ 个。考察 parse tree,当 parse tree 从 root 到 leaf 最深的 path 长度为 $v+2$ 时,至少有一个 variable $N$ 出现了两次,假设 $S\Rightarrow^* uNz\Rightarrow uvNyz\Rightarrow uvxyz$,那么显然也可以有 $S\Rightarrow^* uNz\Rightarrow uvNyz\Rightarrow uvvNyyz\Rightarrow uvvxyyz$。可以算出 $p$ 是 $b,v$ 的一个函数。
可以用 pumping lemma 证明,$\{a^n b^n c^n | n\geq 0\}, \{ww|w\in\{0,1\}^*\}, \{a^i b^j c^k | 0\leq i\leq j\leq k\}$ 都不是 context-free 的。